Evaluation of Riemann flux solvers for WENO reconstruction schemes: Kelvin-Helmholtz instability

Abstract

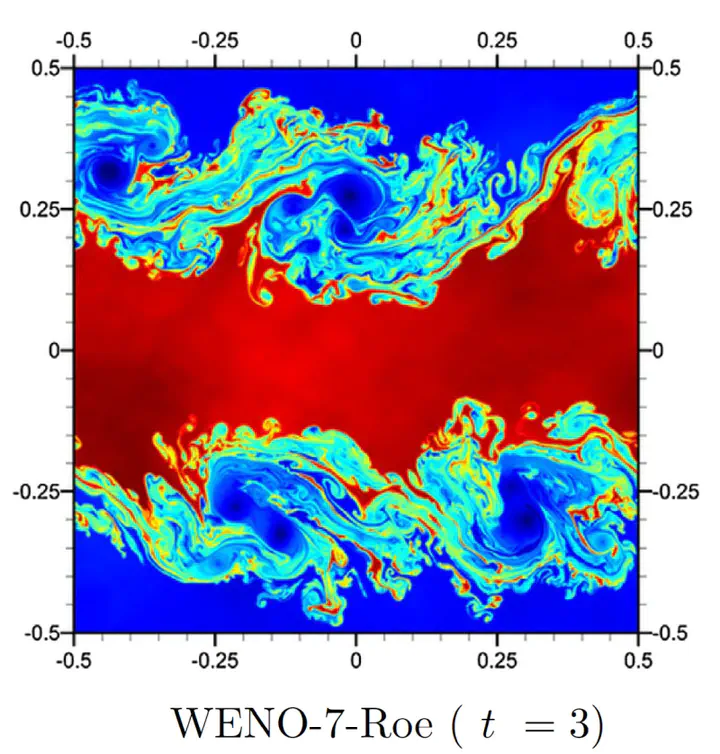
Accurate and computationally efficient simulations of Euler equations are of paramount importance in both fundamental research and engineering applications. In this study, our main objective is to investigate the efficacy and accuracy of several Riemann solvers for high-order accurate weighted essentially non-oscillatory (WENO) reconstruction scheme as a state-of-the-art tool to study shear driven turbulence flows. The Kelvin–Helmholtz instability occurs when a perturbation is introduced to a continuous fluid system with a velocity shear, or where there is a velocity difference across the interface between two fluids. Here, we solve a stratified Kelvin–Helmholtz instability problem to demonstrate the performance of six different Riemann solvers’ ability to evolve a linear perturbation into a transition to nonlinear hydrodynamic two-dimensional turbulence. A single mode perturbation is used for our evaluations. Time evolution process shows that the vortices formed from the turbulence slowly merge together since both energy and enstrophy are simultaneously conserved in two-dimensional turbulence. Third-, fifth- and seventh-order WENO reconstruction schemes are investigated along with the Roe, Rusanov, HLL, FORCE, AUSM, and Marquina Riemann flux solvers at the cell interfaces resulting in 18 joint flow solvers. Based on the numerical assessments of these solvers on various grid resolutions, it is found that the dissipative character of the Riemann solver has significant effect on eddy resolving properties and turbulence statistics. We further show that the order of the reconstruction scheme becomes increasingly important for coarsening the mesh. We illustrate that higher-order schemes become more effective in terms of the tradeoff between the accuracy and efficiency. We also demonstrate that AUSM solver provides the least amount of numerical dissipation, yet resulting in a pile-up phenomenon in energy spectra for underresolved simulations. However, results obtained by the Roe solver agree well with the theoretical energy spectrum scaling providing a marginal dissipation without showing any pile-up at a cost of around 30% increase in computational time.

Kursat Kara

Assistant Professor, Mechanical and Aerospace Engineering

Dr. Kara is the principal investigator of the Kara Aerodynamics Research Laboratory at Oklahoma State University. He teaches the Fundamentals of Aerodynamics, Unsteady Aerodynamics, Computational Fluid Dynamics, and Quantum Computing. Previously, he was an assistant professor at Khalifa University, where he received the Faculty Excellence Award for Outstanding Teaching in 2015.