Numerical assessments of high-order accurate shock capturing schemes: Kelvin–Helmholtz type vortical structures in high-resolutions

Abstract

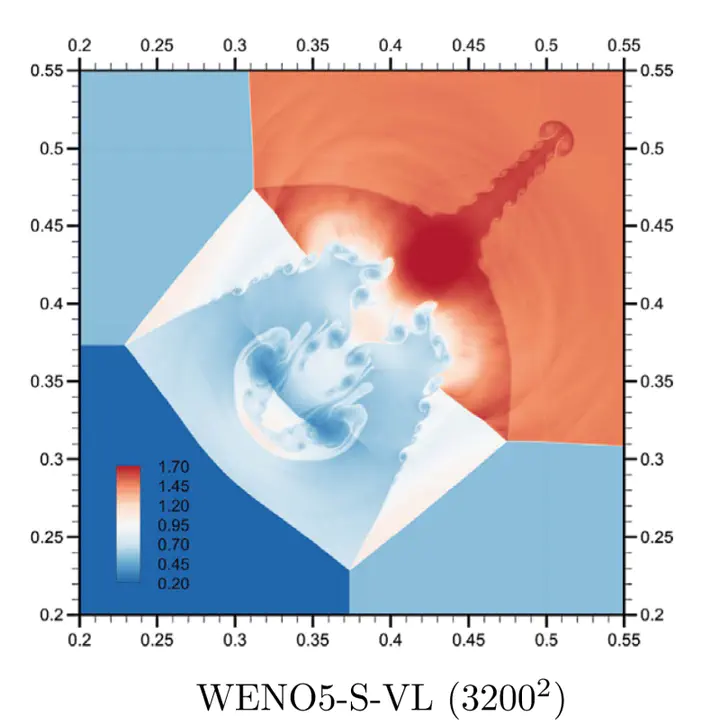
This paper investigates the performance of extensions of the state-of-the-art high-resolution shock-capturing schemes by solving hyperbolic conservation laws in gas dynamics. Such numerical methods used to integrate compressible flow simulations should provide accurate solutions for these flows’ long-time integrations. To this end, several joint solvers are developed within the framework of the reconstruction and flux-splitting approaches using the underlying MUSCL and WENO frameworks. The numerical assessments include testing and evaluation of various interpolation procedures, flux-limiters, Riemann solvers, flux-splitting schemes, and their formal order of accuracy. For temporal integration, a three-stage optimal TVD Runge–Kutta time stepping is employed. The modular development of these joint solvers provides ease in characterizing the solution procedures. The performances of these high-resolution solvers are compared for several carefully selected two-dimensional Riemann problems, including shock and rarefaction waves and joint discontinuities. Based on solutions obtained by all five-point stencil schemes, we demonstrate that the reconstruction-based WENO scheme with the Roe solver is more accurate than all the versions of the flux-splitting WENO solvers tested in this study. We also show that results are highly dependent on the choice of the flux limiter. It is shown that the Euler equations discretized by the fifth-order WENO scheme produce solutions that convect vorticity and create small-scale vortical flow structures, which are usually associated with the high Reynolds number viscous flows. Surprisingly, it is found that these Kelvin–Helmholtz instability-like vortical structures are not captured in any form of the third-order five-point stencil schemes.

Kursat Kara

Assistant Professor, Mechanical and Aerospace Engineering

Dr. Kara is the principal investigator of the Kara Aerodynamics Research Laboratory at Oklahoma State University. He teaches the Fundamentals of Aerodynamics, Unsteady Aerodynamics, Computational Fluid Dynamics, and Quantum Computing. Previously, he was an assistant professor at Khalifa University, where he received the Faculty Excellence Award for Outstanding Teaching in 2015.